In order to explain the “internal value” of an option, we will assume that the option can be exercised at any time, as in the case of an American option.
The “internal value” of an option, at any point in time, is equal to the profit we would gain from exercising the option at that time (gross profit).
If exercising the option on a particular date does produce a profit, this means: the option has no internal value (Internal value = 0).
Calculating the internal value:
For a Call option – the difference between the market price and the exercise price.
For a Put option – the difference between the exercise price and the market price.
The internal value changes with any change in the market price.
No internal value:
In the following cases, there is no internal value:
On a Call option: When the exercise price is equal to or higher than the market price.
On a Put option: When the market price is equal to or higher than the exercise price.
Internal value as the basis for calculating the premium
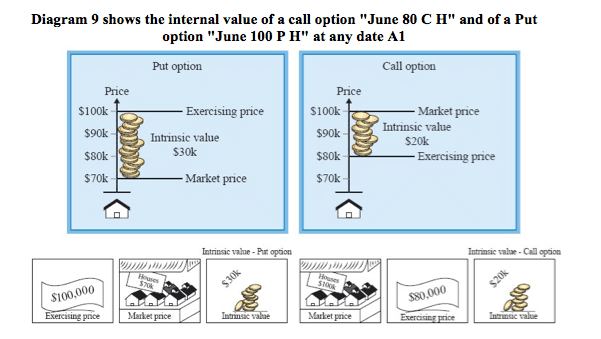
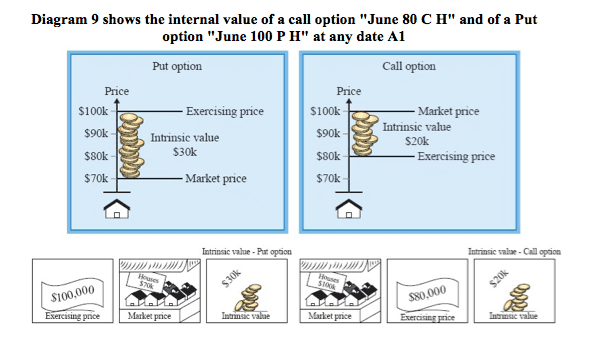
The internal value should be the basis for calculating the premium. It is unreasonable that the premium would be less than the internal value of the option. We can explain this by means of the Diagram 9.
Call option
Let us assume we are holding an option “June $80K C H”.
If we sell the option for less than $20K, we will lose money, since we can exercise it and make a profit of $20K. (For the purposes of the explanation, we assume this to be an American option which can be exercised at any point in time).
Put option
Let us assume we are holding an option “June $100K P H”.
If we sell the option for less than $30K, we will lose money, since we can exercise it and make a profit of $30K.
In fact, whoever sells an option at a premium which is equal to its internal value, is swapping money for money, since he receives, on the one hand, a premium, and on the other hand, hands over an asset which includes a profit in the same amount.