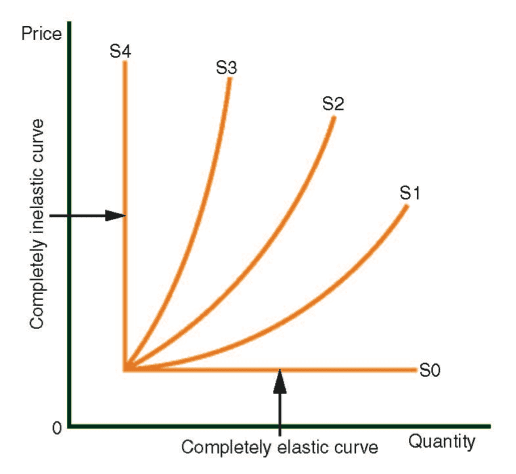
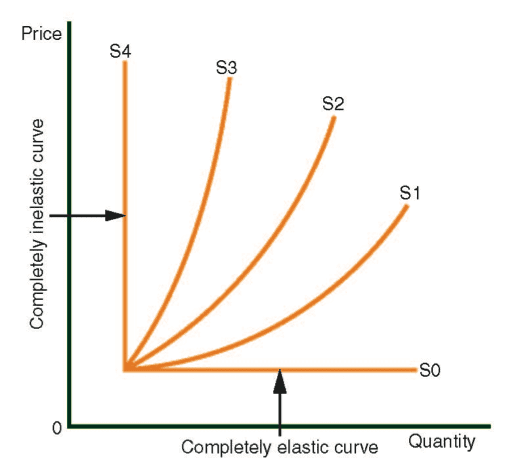
Elasticity of the Supply and Demand Curves

The elasticity of a curve refers to its slope. As a curve becomes more horizontal (flat) it becomes more elastic. If a curve becomes more upright (vertical), or moves towards a vertical position, we call it inelastic. The more vertical the curve, then the more inelastic it is. 

If a curve is completely horizontal, then we say it is complerely elastic. 

If a curve is completely vertical, then it is said to be completely inelastic.

The following digrams display the elasticity of five demand curves and five supply curves in various modes.

Demand curve D1 is somewhat more elastic than D2, and it is definitely more elastic than D3 and D4. Supply Curve S1 is somewhat more elastic than S2, and it is definitely more elastic than S3 and S4.

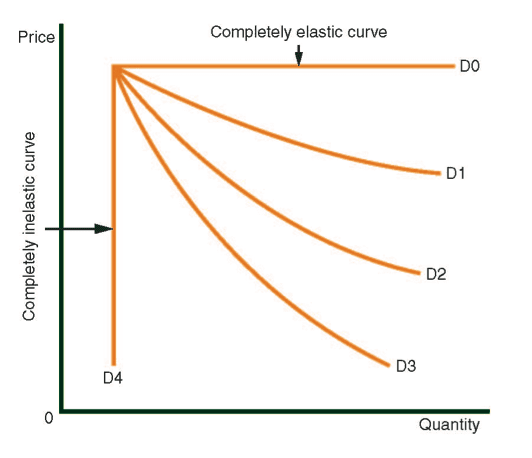
Levels of Elasticity

The demand curve:

The following diagrm shows demand curves for shoes in three different countries: 

• Demand curve D1 is for Country A. 
• Demand curve D2 is for Country B. 
• Demand curve D3 is for Country C. 

Demand curves for shoes in three countries

 

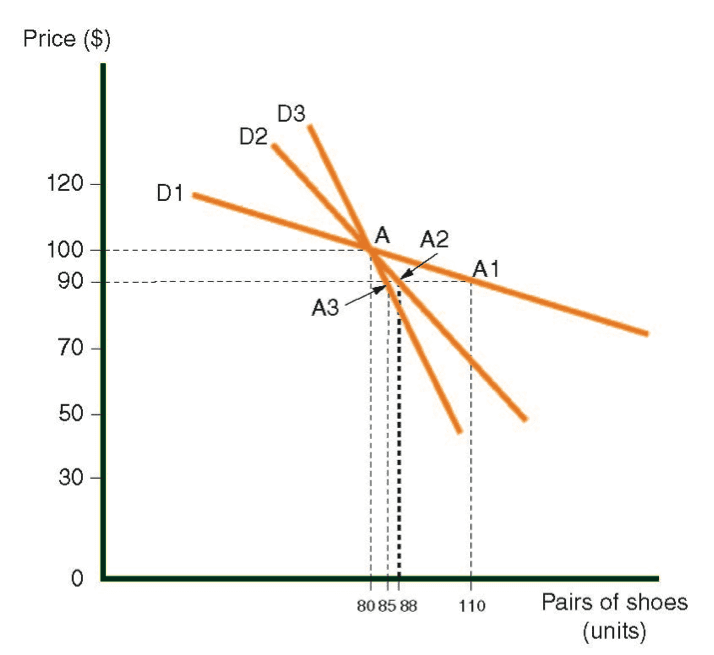
For the purposes of this explanation, assume that point A is common to all three demand curves. At point A, the price is $100 and the demand equal 80 units. Consider what happens when the price of shoesfalls 10% (from $100 to $90).

In Country A: point A1 indicates the new situation. When the price falls by 10% (to $90), then demand rises from 80 to 110, i.e., a 37.5% increase. In other words, a 1% drop in price causes a 3.75% increase in consumer demand. 

In Country B: point A2 indicates the new situation. When the price falls by 10%, then demand rises from 80 to 88, which would be a 10% increase. In other words, a 1% drop in price result in a 1% increase in demand. 

In Country C: point A3 indicates the new situation. When the price falls by 10%, then the demand rises from 80 to 84, which represents a 5% increase. In other words, a 1% drop in price causes a 0.5% increase in demand.

Summary of Changes in the Demand Curve for Shoes:

Curve D1 – (on average) a 1% drop in price boosts demand by 3.75%. 

Curve D2 – (on average) a 1% drop in price boosts demand by 1%. 

Curve D3 – (on average) a 1% drop in price boosts demand by 0.5%

Categorizing Curves by their Slope

1. When a 1% change in price alters demand by more than 1%, as in the case of D1, we say that the curve is elastic. In general when a change in price alters  demand by a greater proportion than the change in price, we say that the curve is elastic. 
2. When a 1% change in price alters demnd by less than 1%, as in the case of D3, we say that the curve is inelastic. In general, when a change in price alters demand by a lower proportion than the change in price, we say that the curve is inelastic. 
3. When a 1% change in price changes demand by exactly 1%, as in the case of D2, we say that curve in parity. In general, when a change in price causes the same proportion of change in demand, we say that the curve in parity.

A Few Improvements for the Sake of Accuracy

1. Point-specific elasticity: When evaluating the elasticity of a curve, it is necessary to focus upon a specific point on the curve since elasticity varries depending upon its position on the curve. Without reference to  specific point on the curve, the term elasticity would have no meaning.
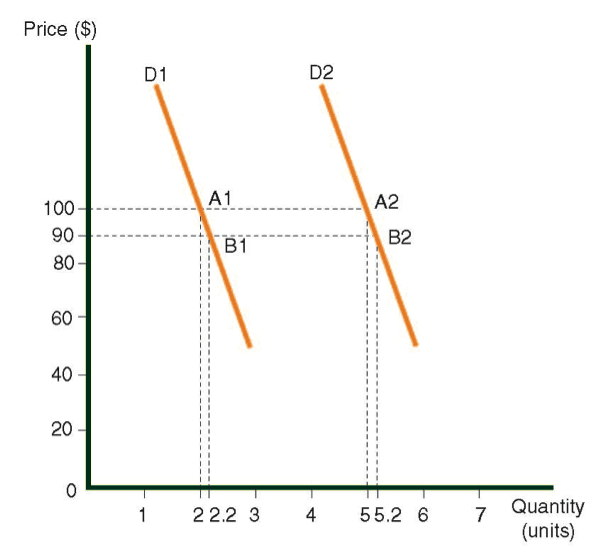
2. The slope of the curve is not the only influence on the degree of elasticity: Althrough it was stated previously that the elasticity of a curve is  way of desribing the steepness of its slope, this statement is an oversimplication for purposes of explaining the concept, i.e., it is not entirely accurate. The following diagram displays two parallel demand curves, D1 and D2, each with the same slope. 

This diagram shows that two curves with the same slope can differ in terms of their elasticity. 

The elasticity of the curve D1 at point A1 (price $100, quantity 2) and elasticity of the curve D2 at point A2 (price $100, quantity 5) are calculated as follows: For each of the curves, let the price be reduced from $100 to $90 (-10%). As a result, the amount of demand for each of the curves rises as follows: 

Curve D1: From 2 to 2.2 (+10%), with point B1 representing the new situation. 

Curve D2: From 5 to 5.2 (+4%) with point B2 representing the new situation.  

Calculation of the elasticity for each of the curves: 

Curve D1: Unit elasticity  = +10% (change in quantity)/-10% (change in price) = 1.0

Curve D2: Inelasticity   = +4% (change in quantity)/-10% (change in price) = 0.4 

Conclusion:

Elasticity at Point A₁ is 1, while elasticity at Point A₂ is 0.4.

We start by measuring elasticity at Point A1 on Curve D1, which is followed by Point A2 on Curve D2.

The slope is (sometimes) more important:

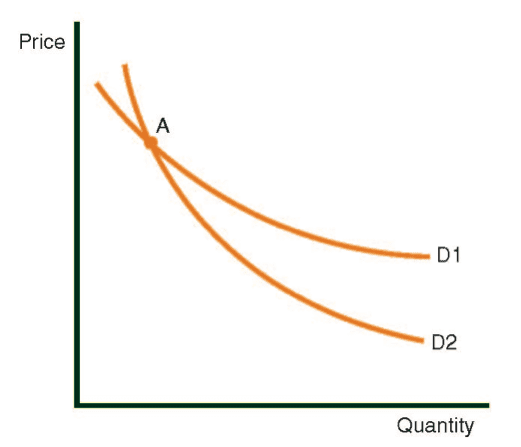
When two curves intersect at a specific point – for example in the following diagram at point A on Curves D1 and D2 – it can be said that D1 is more elastic than D2 at that point. If prices drop by 1%, then demand on Curve D2 will increase by a%, while demand on Curve D1 will rise by (a+b)%. This shows that D1 is more elastic.

Using the Word Change, Instead of Increase or Decrease

In order to illustrate the meaning of elasticity, we began with an example that explored the rise in demand caused by a reduction in the price of specific product. We emphasize that it is more accurate to say that elasticity measures the change in demand caused by  a change in price; so, it makes no difference whether the price rises or falls, or whether demand increases or decreases. The precise formula for elasticity is as follows:

Elasticity =  % Change in price/ % Change in demand